Aliasing on Purpose

We say something is aliased when it has more than one name. Mark Twain is an alias of Samuel Clemens. Banksy is an alias of someone, but at the time of this writing I don’t know who. In software, we interpret “name” in a broad way to mean any way of designating some object. If x names the same object as elements[3], then we say that object is aliased and that x and elements[3] are aliases.

When Aliasing Doesn’t Matter

One reason for making immutable objects is so that we can alias those objects without worry. This is why str objects in Python are immutable. If x refers to a string object, I can set y = x without any worry about the consequence of aliasing the string, because there is nothing I can do to x that will affect y. All the operations on strings, like strip and split, return new objects rather than changing the strings.

There is at least one way that we can observe aliasing with immutable objects: The comparison x is y checks whether x is an alias of y. It can yield some surprises. For example, Python sometimes aliases int values that are equal, and sometimes doesn’t:

PyDev console: starting.
Python 3.8.0 (v3.8.0:fa919fdf25,...)
>>> w = 5
>>> x = 5
>>> w is x
True
>>> w = 1000
>>> x = 1000
>>> w is x
False

As long as we use == instead of is, we need not be concerned about whether int values or str values are aliased. When we define our own immutable classes, we aim for similar behavior: The == (that is __eq__) operation should define what we mean by “same”, and aliasing (is) should be irrelevant.

When Aliasing is a Mistake

While immutable objects are often convenient, sometimes they are impractical. For example, the list class in Python is mutable because the append operation would be too expensive if it returned a new list object; it is much more efficient to modify (mutate) an existing list object. But this means we must be careful:

>>> m = [1, 2, 3]
>>> k = m
>>> k.append(4)
>>> print(m)
[1, 2, 3, 4]

This behavior, in which the value designated by one alias of an object is changed by an operation through another alias of the object, may be fine or even useful, but it may also lead to bugs that are difficult to find and correct. This is one reason that our coding style guidelines require us to make it very clear and apparent when a method is a mutator.

We have already seen examples where aliasing a mutable object is a mistake. For example, if Point objects are mutable (if they have a move operation that changes a Point object, instead of returning a new Point object), then aliasing Point objects from different Rect rectangle objects is probably a mistake. At the very least it requires great care to do it correctly, without unanticipated side effects.

When Aliasing is Helpful

While unanticipated side effects can make aliasing a problem, occasionally we alias objects intentionally because we want to access the same objects in more than one way.

Suppose, for example, that we have a list of complex objects storing information about students. Each object representing a student might include a given name, a family name, and a student identification number, among other pieces of information like favorite ice cream flavor. We might want to find student records quickly using binary search for given name, family name, or student number. But binary search only works if the objects are in sorted order, and each of these search keys requires a different order!

Database systems have a simple solution to the problem of searching for the same objects by multiple keys: They keep multiple indexes with aliased references to the records.

While search structures are the most common intentional use of aliasing, it is also useful sometimes for refactoring program logic.

Consider the simple game known as noughts and crosses or tic tac toe. Suppose the game board is represented by a list of lists of Tile objects, using letters a through i as position labels.

class Board:
    """Simple 3x3 Tic Tac Toe board"""
    def __init__(self):
        self.tiles = [[Tile('a'), Tile('b'), Tile('c')],
                      [Tile('d'), Tile('e'), Tile('f')],
                      [Tile('g'), Tile('h'), Tile('i')]]

A game of noughts and crosses is won when there are three X or three O on tiles in any row, column, or diagonal. We might use an Enum to represent the X and O marks:

class Mark(Enum):
    xmark = "X"
    omark = "O"
    unmarked = "."

The logic for checking for a win in a row might look something like this:

def row_is_winner(self, row_index) -> bool:
    mark_0 = self.tiles[row_index][0].mark
    mark_1 = self.tiles[row_index][1].mark
    mark_2 = self.tiles[row_index][2].mark
    if mark_0 == Mark.unmarked: 
        return False
    return mark_0 == mark_1 and mark_1 == mark_2

The logic for checking for a win in a column might look very similar:

def row_is_winner(self, col_index) -> bool:
    mark_0 = self.tiles[0][col_index].mark
    mark_1 = self.tiles[1][col_index].mark
    mark_2 = self.tiles[2][col_index].mark
    if mark_0 == Mark.unmarked: 
        return False
    return mark_0 == mark_1 and mark_1 == mark_2

Checking a diagonal would be yet again almost the same logic on different sets of tiles.

Similar as these functions are, it is difficult to combine them if the Tile objects are arranged only in the single list-of-lists structure by row and column. The logic can be factored easily, though, if we alias the same set of tiles from groups for rows, columns, and diagonals.

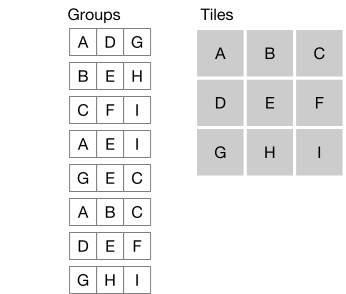
Now it is simple to write a single function to check whether a group is a winner:

def is_winner(group: List[Tile]) -> bool:
    """True if a win for *either* X or O"""
    q, r, s = group
    return (q.mark != Mark.unmarked
            and q.mark == r.mark
            and r.mark == s.mark)

It is easy to check all the rows, columns, and diagonals with a single loop:

    def has_winner(self) -> bool:
        """There is some winning row or column (for either X or O)"""
        for group in self.groups:
            if is_winner(group):
                return True
        return False

We have not really removed the complexity of traversing the board in three different orders, because we must traverse it to build the tile groups that represent those different orders.

    def __init__(self):
        self.tiles = [[Tile('a'), Tile('b'), Tile('c')],
                      [Tile('d'), Tile('e'), Tile('f')],
                      [Tile('g'), Tile('h'), Tile('i')]]
        # 3-in-a-row can be horizontal, vertical, or diagonal
        self.groups = []
        # horizontal
        for row in self.tiles:
            self.groups.append(row)
        # vertical
        for col_i in range(3):
            group = []
            for row_i in range(3):
                group.append(self.tiles[row_i][col_i])
            self.groups.append(group)
        # diagonal left-to-right
        self.groups.append([self.tiles[i][i] for i in range(3)])
        # diagonal right-to-left
        self.groups.append([self.tiles[i][2-i] for i in range(3)])

However, we need do that only once, as we do here in the constructor. We can separate that logic from the logic of checking for a winner. The advantage becomes much larger if we use the groups in additional ways involving different logic. For example, we might write another function to choose a tile to mark with an X or O, selecting the best move by using the same groups.

    def choose_for(self, mark: Mark) -> str:
        """Returns the most worthwhile position for
        mark to take, assuming it is the turn for
        mark and that there are open positions.
        """
        # We use the 'worth' field of the tiles to tally
        # how valuable each position is.
        for row in self.tiles:
            for col in row:
                col.worth = 0
        for group in self.groups:
            worth = calc_worth(group, mark)
            for tile in group:
                # No harm in granting worth to marked tiles
                tile.worth += worth
        # Pick open tile with max worth
        all_tiles = self.tiles[0] + self.tiles[1] + self.tiles[2]
        open_tiles = [tile for tile in all_tiles if tile.mark == Mark.unmarked]
        open_tiles.sort(key=lambda tile: tile.worth, reverse=True)
        return open_tiles[0].name

Notice that in the above method, we are looping through the same set of tiles in different ways. We first loop through by row and column to initialize the worth fields. Then we loop through them in multiple orders using the groups, which refer to the very same Tile objects ordered by row, column, and diagonal.

Note also that a single tile will be accessed multiple times in different groups, potentially accumulating worth each time it is accessed. On the initially empty board, a middle tile along one side will be accessed once in a row group and once in a column group, accumulating a total worth of 2.

A corner tile accumulates worth from a row group, a column group, and a diagonal group, because it can be used to form winning combinations in each of those groupings:

Alternatives

The groups structure for aliasing groups of tiles in different orders is not the only way we could arrange different access orders for the tiles.
We could have written methods or functions to return lists of tiles in the desired order each time we needed them. Python also provides generators, which are identical to functions except they may return several results, one at a time. (The range function is actually a generator; it returns elements of the range one by one, not all together in a list.)

The main advantage of building the groups structure is that we only build it once, and then use it several times.

Summary

If there is more than one way of designating (“naming”) the same object, we say the object is “aliased”. Aliasing immutable objects usually has no observable effect, and often we design objects to be immutable so that we can alias them freely. We must be careful when aliasing mutable objects, because a change to the object through one “name” will be observable as a change to the object through any other “names” it may have.

While aliasing can dangerous, it can also be useful. Sometimes we need different ways to designate the same set of objects, as when we traverse a collection repeatedly in different orders. And sometimes making a change to an object accessed through one name visible when the same object is accessed through other names is exactly what we want. We illustrated this by accumulating the “worth” of game tiles accessed in different orders.