Objects

In Python, objects are used to represent information. Every variable you use in a Python program is a reference to an object. The values you have been using so far – numbers, strings, dicts, lists, etc – are objects. They are among the built-in classes of Python, i.e., kinds of value that are already defined when you start the Python interpreter.

You are not limited to those built-in classes. You can use them as a foundation to build your own.

Example: Points

What if we wanted to define a new kind of value? For example, if we wanted to write a program to draw a graph, we might want to work with cartesian coordinates, representing each point as an (x,y) pair. We might represent the point as a tuple like (5,7), or we could represent it as the list [5, 7], or we could represent it as a dict {"x": 5, "y": 7}, and that might be satisfactory. If we wanted to represent moving a point (x,y) by some distance (dx, dy), we could define a a function like

def move(p, d):
    x,y = p
    dx, dy = d
    return (x+dx, y+dy)
    
pt_1 = (5,8)
pt_2 = move(pt_1, (3,7))
print(pt_2)

(8, 15)

But if we are making a graphics program, we’ll need to move functions for other graphical objects like rectangles and ovals, so instead of naming it move we’ll need a more descriptive name like move_point. Also we should give the type contract for the function, which we can do with Python type hints. With these changes, we get something like this

from typing import Tuple
from numbers import Number

def move_point(p: Tuple[Number, Number],
               d: Tuple[Number, Number]) \
        -> Tuple[Number, Number]:
    x, y = p
    dx, dy = d
    return (x+dx, y+dy)
    
move_point((3,4),(5,6))

(8, 10)

Can we do better?

We aren’t really satisfied with using tuples to represent points. What we’d really like is to express the concept of adding two points more concisely, as (3,4) + (5,6). What would happen if we tried this?

(3,4) + (5,6)

(3, 4, 5, 6)

That’s not what we wanted! Would it be better if we represented points as lists?

[3,4] + [5,6]

[3, 4, 5, 6]

No better. Maybe as dicts?

{"x": 3, "y": 4} + {"x": 5, "y": 6}

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[5], line 1
----> 1 {"x": 3, "y": 4} + {"x": 5, "y": 6}

TypeError: unsupported operand type(s) for +: 'dict' and 'dict'

That is not much of an improvement, although an error message is usually better than silently producing a bad result. What we really want is not to use one of the existing representations like lists or tuples or dicts, but to define a new representation for points.

A new representation

Each data type in Python, including list, tuple, and dict, is defined as a class from which objects can be constructed. We can also define our own classes, to construct new kinds of objects.
For example, we can make a new class Point to represent points.

class Point:
    """An (x,y) coordinate pair"""

Inside the class we can define methods, which are like functions that are specialized for the new representation. The first method we should define is a constructor with the name __init__. The constructor describes how to create a new Point object:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y
        
p = Point(5,3)

print(f"p has x coordinate {p.x} and y coordinate {p.y}")

p has x coordinate 5 and y coordinate 3

Instance variables

Notice that the first argument to the constructor method is self, and within the method we refer to self.x and self.y. In a method that operates on some object o, the first argument to the method will always be self, which refers to the whole object o. Within the self object we can store instance variables, like self.x and self.y for the x and y coordinates of a point. When we use the Point object p from outside the class, we refer to those elements as p.x and p.y, as in the print statement above.

Methods

What about defining an operation for moving a point? Instead of adding _point to the name of a move function, we can just put the function (now called a method) inside the Point class:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y

    def move(self, d: "Point") -> "Point":
        """(x,y).move(dx,dy) = (x+dx, y+dy)"""
        x = self.x + d.x
        y = self.y + d.y
        return Point(x,y)

Notice that the instance variables self.x and self.y we created in the constructor can be used in the move method. They are part of the object, and can be used by any method in the class. The instance variables of the other Point object d are also available in the move method. Let’s look at how these objects are passed to the move method.

Method calls

Next we’ll create two Point objects and call the move method to create a third Point object with the sums of their x and y coordinates:

p = Point(3,4)
v = Point(5,6)
m = p.move(v)

print(f"m has x coordinate {m.x} and y coordinate {m.y}")

m has x coordinate 8 and y coordinate 10

At first it may seem confusing that we defined the move method with two arguments, self and d, but it looks like we passed it only one argument, v. In fact we passed it both points: p.move(v) passes p as the self argument and v as the d argument. We use the variable before the ., like p in this case, in two different ways: To find the right method (function) to call, by looking inside the class to which p belongs, and to pass as the self argument to the method.

The move method above returns a new Point object at the computed coordinates. A method can also change the values of instance variables. For example, suppose we add a move_to method to Point:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y

    def move(self, d: "Point") -> "Point":
        """(x,y).move(dx,dy) = (x+dx, y+dy)"""
        x = self.x + d.x
        y = self.y + d.y
        return Point(x,y)
        
    def move_to(self, new_x, new_y):
        """Change the coordinates of this Point"""
        self.x = new_x
        self.y = new_y

m = Point(3,4)
m.move_to(19,23)
print(f"({m.x}, {m.y})")

(19, 23)

Note that the move_to method does not return the moved point. This is a common mistake!

w = m.move_to(19, 23)  # Oops! 
print(w)

# Attempting to access w.x or w.y will fail: 
print(f"w has x coordinate {w.x} and y coordinate {w.y}")

None

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[10], line 5
      2 print(w)
      4 # Attempting to access w.x or w.y will fail: 
----> 5 print(f"w has x coordinate {w.x} and y coordinate {w.y}")

AttributeError: 'NoneType' object has no attribute 'x'

What is self?

Many people are confused by the self variable. The name self is merely a convention in Python. Conventions are important for readability and avoiding errors, so you should never write code like the following, but it may help you to see that there is really nothing special about self aside from convention.

class BadExample():
    """An example in which we use other names instead of "self".
    DON'T DO THIS ... but understand it. 
    """
    
    def __init__(elephant, x: int): 
        elephant.v = x    # Might as well be consistently inconsistent
        
    def increase(zebra, y: int): 
        zebra.v += y
        
wacky = BadExample(17)
wacky.increase(13)
print(wacky.v)

30

As you can see, when we make a method call like wacky.increase(13), the first argument is the object wacky. We ordinarily call that argument self, not because it matters to Python, but because it matters to other programmers who need to read and understand our code.

Check your understanding

Consider class Pet and object my_pet.
What are the instance variables of my_pet? What are the values of those instance variables after executing the code below?

class Pet: 
    def __init__(self, kind: str, name: str):
        self.species = kind
        self.called = name
    
    def rename(self, new_name):
        self.called = new_name

my_pet = Pet("canis familiaris", "fido")

A little magic

We said above that what we really wanted was to express movement of points very compactly, as addition. We saw that addition of tuples or lists did not act as we wanted; instead of (3,4) + (5,6) giving us (8,10), it gave us (3,4,5,6). We can almost get what we want by describing how we want + to act on Point objects. We do this by defining a special method __add__:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y
    
    def move(self, d: "Point") -> "Point":
        """(x,y).move(dx,dy) = (x+dx, y+dy)"""
        x = self.x + d.x
        y = self.y + d.y
        return Point(x,y)
        
    def move_to(self, new_x, new_y):
        """Change the coordinates of this Point"""
        self.x = new_x
        self.y = new_y
        
    def __add__(self, other: "Point"):
        """(x,y) + (dx, dy) = (x+dx, y+dy)"""
        return Point(self.x + other.x, self.y + other.y)

Special methods are more commonly known as magic methods. They allow us to define how arithmetic operations like + and - work for each class of object, as well as comparisons like < and ==, and some other operations.
If p is a Point object, then p + q is interpreted as p.__add__(q). So finally we get a very compact and readable notation:

p = Point(3,4)
v = Point(5,6)
m = p + v

print(f"({m.x}, {m.y})")

(8, 10)

More: Appendix on magic methods

Magic for printing

Suppose we wanted to print a Point object. We could do it with an f-string, as we have above:

print(f"p is ({p.x}, {p.y})")

p is (3, 4)

That would give us a reasonable printed representation, like “p is (3, 4)”, but it is tedious, verbose, and easy to get wrong. What if we just wrote

print(f"p is {p}")

p is <__main__.Point object at 0x103f2eba0>

That isn’t a very useful way to print an object!

str()d, not shaken

If we want to print Point objects as simply as we print strings and numbers, but we want the printed representation to be readable, we will need to write additional methods to describe how a Point object should be converted to a string.

In fact, in Python we normally write two magic methods for this: __str__ describes how it should be represented by the str() function, which is the representation used in print or in an f-string like f"it is {p}". We might decide that we want the object created by Point(3,2) to print as “(3, 2)”. We would then write a __str__ method in the Point class like this:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y
    
    def move(self, d: "Point") -> "Point":
        """(x,y).move(dx,dy) = (x+dx, y+dy)"""
        x = self.x + d.x
        y = self.y + d.y
        return Point(x,y)
        
    def move_to(self, new_x, new_y):
        """Change the coordinates of this Point"""
        self.x = new_x
        self.y = new_y
        
    def __add__(self, other: "Point"):
        """(x,y) + (dx, dy) = (x+dx, y+dy)"""
        return Point(self.x + other.x, self.y + other.y)

    # Two new methods, used by the "str" and "repr"
    # functions. 
  
    def __str__(self) -> str:
        """Printed representation.
        str(p) is an implicit call to p.__str__()
        """
        return f"({self.x}, {self.y})"
      
    def __repr__(self) -> str:
        """Debugging representation.  This is what
        we see if we type a point name at the console.
        """
        return f"Point({self.x}, {self.y})"

Now if we again execute

p = Point(17,13)
print(f"p is {p}")

p is (17, 13)

we get a more useful result.

A repr() for debugging

Usually we will also want to provide a different string representation that is useful in debugging and at the Python command line interface. The string representation above may be fine for end users, but for the software developer it does not differentiate between a tuple (3, 4) and a Point object (3, 4). We can define a __repr__ method to give a string representation more useful in debugging. The function repr(x) is actually a call on the __repr__ method of x, i.e., x.__repr__().

Although Python will permit us to write whatever __repr__ method we choose, by accepted convention is to make it look like a call on the constructor, i.e., like Python code to create an identical object. Thus, for the Point class we might write:

    def __repr__(self) -> str:
        return f"Point({self.x}, {self.y})"

Now we can write

print(f"repr(p) is {repr(p)}")

repr(p) is Point(17, 13)

More often, the repr function is called implicitly when we just enter an expression at the console.

p + m

Point(25, 23)

The print function automatically applies the str function to its arguments, so defining a good __str__ method will ensure it is printed as you like in most cases. Oddly, though, the __str__ method for list applies the __repr__ method to each of its arguments, which we can see by writing

p = Point(22, 17)
v = Point(18, 13)
print(p)
print(v)
print([p, v])

(22, 17)
(18, 13)
[Point(22, 17), Point(18, 13)]

Check your understanding

Which of the following are legal, and what values do they return?

• str(5)

• (5).str()

• (5).__str__()

• __str__(5)

• repr([1, 2, 3])

• [1, 2, 3].repr()

• [1, 2, 3].__repr__()

What does the following little program print?

class Wrap: 
    def __init__(self, val: str):
        self.value = val

    def __str__(self) -> str:
        return self.value

    def __repr__(self) -> str:
        return f"Wrap({self.value})"

a = Wrap("alpha")
b = Wrap("beta")
print([a, b])

Variables refer to objects

Before reading on, try to predict what the following little program will print.

x = [1, 2, 3]
y = x
y.append(4)
print(x)
print(y)

Now execute that program. Did you get the result you expected? If it surprised you, try visualizing it in PythonTutor (http://pythontutor.com/). You should get a diagram that looks like this:

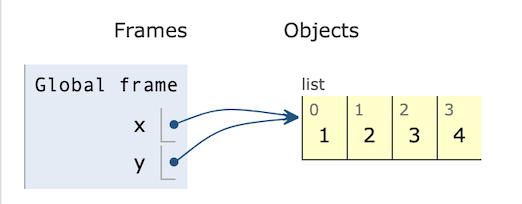
x and y are distinct variables, but they are both references to the same list. When we change y by appending 4, we are changing the same object that x refers to. We say that x and y are aliases, two names for the same object.

Note this is very different from the following:

x = [1, 2, 3]
y = [1, 2, 3]
y.append(4)
print(x)
print(y)

Each time we create a list like [1, 2, 3], we are creating a distinct list. In this seocond version of the program, x and y are not aliases.

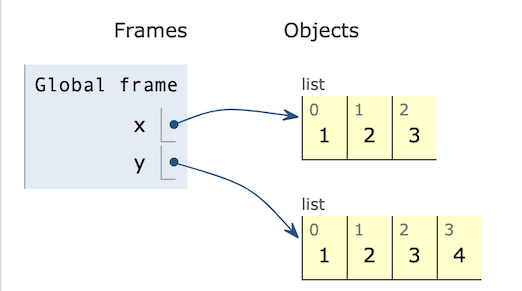
It is essential to remember that variables hold references to objects, and there may be more than one reference to the same object. We can observe the same phenomenon with classes we add to Python. Consider this program:

p1 = Point(3,5)
p2 = p1
p1.move_to(7, 9)
print(p2)

(7, 9)

Once again we have created two variables that are aliases, i.e., they refer to the same object. PythonTutor illustrates:

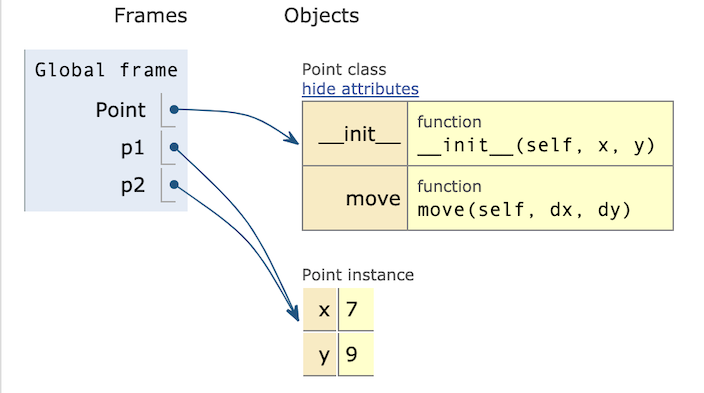
Note that Point is a reference to the class, while p1 and p2 are references to the Point object we created from the Point class. When we call p1.move, the move method of class Point makes a change to the object that is referenced by both p1 and p2. We often say that a method like move mutates an object.

There is another way we could have written a method like move.
Instead of mutating the object (changing the values of its fields x and y), we could have created a new Point object at the modified coordinates:

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: int, y: int):
        self.x = x
        self.y = y

    def moved(self, dx: int, dy: int) -> "Point":
        return Point(self.x + dx, self.y + dy)

p1 = Point(3,5)
p2 = p1
p1 = p1.moved(4,4)
print(p1.x, p1.y)
print(p2.x, p2.y)

7 9
3 5

Notice that method moved, unlike method move in the prior example, return a new Point object that is distinct from the Point object that was aliased. Initially p1 and p2 may be aliases, after p2 = p1:

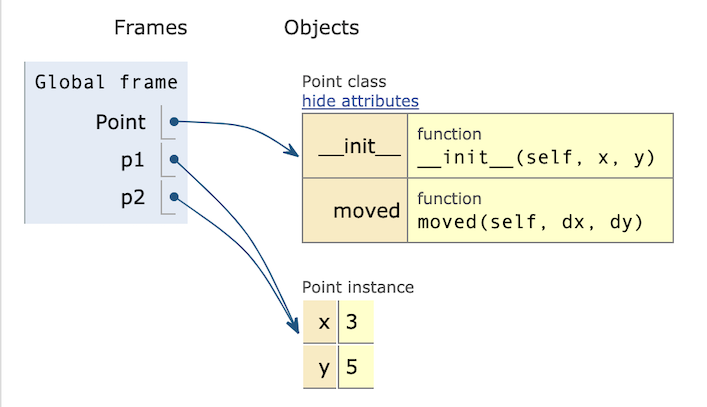
But after p1 = p1.moved(4,4), p1 refers to a new, distinct object:

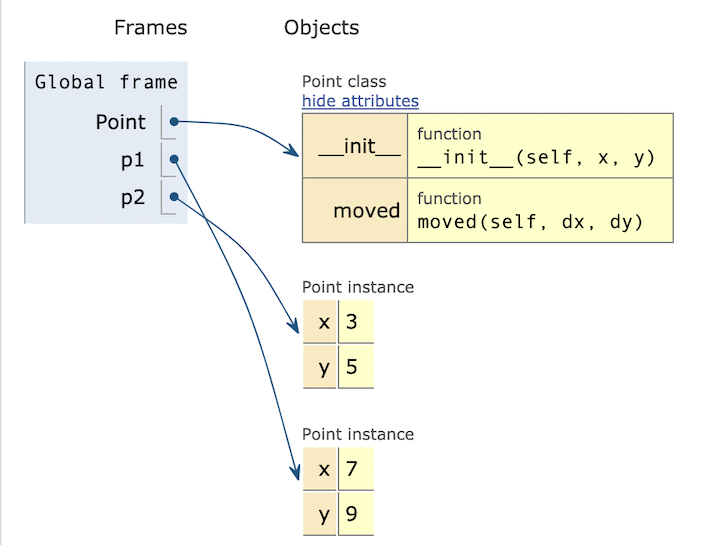
As we saw with the list example, aiasing applies to objects from the built-in Python classes as well as to objects from the classes that you will write. It just hasn’t been apparent until now, because many of the built-in classes are immutable: They do not have any methods that change the values stored in an object. For example, when we write 3 + 5, we are actually calling (3).__add__(5); The __add__ method does not change the value of 3 (that would be confusing!) but instead returns a new object 8.

We will write both immutable and mutable classes.
Aliasing of mutable objects is often a mistake, but not always. Later we will intentionally created aliases to access mutable objects. The important thing is to be aware of it.

Combining Objects: Composing

The instance variables defined in a class and stored in the objects of that class can themselves be objects. We can make lists of objects, tuples of objects, etc.

Often we will want to create a new class with instance variables that are objects created from classes that we have previously created. For example, if we create a new class Rect to represent rectangles, we might want to use Point objects to represent two corners of the rectangle:

Show code cell content Hide code cell content

class Point:
    """An (x,y) coordinate pair"""
    def __init__(self, x: Number, y: Number):
        self.x = x
        self.y = y
    
    def move(self, d: "Point") -> "Point":
        """(x,y).move(dx,dy) = (x+dx, y+dy)"""
        x = self.x + d.x
        y = self.y + d.y
        return Point(x,y)
        
    def move_to(self, new_x, new_y):
        """Change the coordinates of this Point"""
        self.x = new_x
        self.y = new_y
        
    def __add__(self, other: "Point"):
        """(x,y) + (dx, dy) = (x+dx, y+dy)"""
        return Point(self.x + other.x, self.y + other.y)

    def __str__(self) -> str:
        """Printed representation.
        str(p) is an implicit call to p.__str__()
        """
        return f"({self.x}, {self.y})"
      
    def __repr__(self) -> str:
        """Debugging representation.  This is what
        we see if we type a point name at the console.
        """
        return f"Point({self.x}, {self.y})"

class Rect:
    """A rectangle is represented by a pair of points
    (x_min, y_min), (x_max, y_max) at opposite corners.
    Whether (x_min, y_min) is lower left or upper left
    depends on the coordinate system.
    """
    def __init__(self, xy_min: Point, xy_max: Point):
        self.min_pt = xy_min
        self.max_pt = xy_max
    
    def area(self) -> Number:
        """Area is height * width"""
        height = self.max_pt.x - self.min_pt.x
        width = self.max_pt.y - self.min_pt.y
        return height * width

    def translate(self, delta: Point) -> "Rect":
        """New rectangle offset from this one by delta as movement vector"""
        return Rect(self.min_pt + delta, self.max_pt + delta)

    def __repr__(self) -> str:
        return f"Rect({repr(self.min_pt)}, {repr(self.max_pt)}"

    def __str__(self) -> str:
        return f"Rect({str(self.min_pt)}, {str(self.max_pt)})"

p1 = Point(3,5)
p2 = Point(8,7)
r1 = Rect(p1, p2)
mvmt = Point(4, 5)
r2 = r1.translate(mvmt)  # Treat Point(4,5) as (dx, dy)
print(f"{r1} + {mvmt} => {r2}")
print(f"Area of {r1} is {r1.area()}")

Rect((3, 5), (8, 7)) + (4, 5) => Rect((7, 10), (12, 12))
Area of Rect((3, 5), (8, 7)) is 10

Note that the height and width are local variables that exist only while method area is executing. min_pt and max_pt, on the other hand, are instance variables that are stored within the Rect object.

Check your understanding

Suppose we ran the above code in PythonTutor. (PythonTutor cannot import Number, but for the examples we could replace it with int.) What picture would it draw of r1? Would height and width in method area be included as instance variables? Why or why not?

Wrapping and delegation

Sometimes we want a class of objects that is almost like an existing class, but with a little extra information or a few new methods. One way to do this is to build a new class that wraps an existing class, often a built-in class like list or dict. (In the next chapter we will see another approach.)

Suppose we wanted objects that provide some of the same functionality as list objects, and also some new functionality or some restrictions. For example, we might want a method area that returns the sum of the areas of all the Rect objects in the RectList:

class RectList:
    """A collection of Rects."""

    def __init__(self):
        self.elements = [ ]

    def area(self) -> Number:
        total = 0
        for el in self.elements:
            total += el.area()
        return total

That seems reasonable, but how do we add Rect objects to the Rectlist?

We do not want to do it this way:

li = RectList()
# DON'T DO THIS
li.elements.append(Rect(Point(3,3), Point(5,7)))
li.elements.append(Rect(Point(2,2), Point(3,3)))

As a general rule, we should be cautious about accessing the instance variables of an object outside of methods of the object’s class, and we should especially avoid modifying instance variables anywhere except in methods. Code that “breaks the abstraction”, like the example above calling the append method of the elements instance variable, is difficult to read and maintain. So we want instead to give RectList it’s own append method, so that we can write

li = RectList()
li.append(Rect(Point(3,3), Point(5,7)))
li.append(Rect(Point(2,2), Point(3,3)))
print(f"Combined area is {li.area()}")

The append method can be very simple!

    def append(self, item: Rect):
        """Delegate to elements"""
        self.elements.append(item)

Show code cell content Hide code cell content

class RectList:
    """A collection of Rects."""

    def __init__(self):
        self.elements = [ ]
        
    def append(self, item: Rect):
        """Delegate to elements"""
        self.elements.append(item)

    def area(self) -> Number:
        total = 0
        for el in self.elements:
            total += el.area()
        return total

li = RectList()
li.append(Rect(Point(3,3), Point(5,7)))
li.append(Rect(Point(2,2), Point(3,3)))
print(f"Combined area is {li.area()}")

Combined area is 9

We call this delegation because append method of RectList method
just hands off the work to the append method of class list. When we write a wrapper class, we typically write several such trivial delegation methods.

Wrapping and delegation work well when we want the wrapper class (like RectList in this example) to have a few of the same methods as the wrapped class (list). When we want the new collection class to have all or nearly all the methods of an existing collection, the inheritance approach introduced in the next chapter is more appropriate.